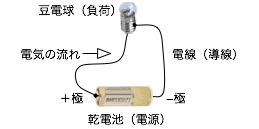
電気(電荷)の通り道として、電線を用意し、それを利用して、電池と抵抗をつないで作った、ぐるっと回る電気の通り道を回路と呼ぶ事は、前回お話しました。

ここでは、少しその回路の性質(1)の話をする事にします。
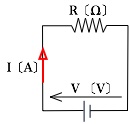
この図では、長い棒と短い棒を組合せたシンボルが下に、上にキザキザと折れまがったシンボルが描かれており、それらが線分で結ばれています。
回路の絵には、電池と、電球があったところには、この図では、それぞれ、特徴的な記号が描かれています。
実は、下の「長い棒と短い棒を組合せた記号」は電池(長い方が+極で、短い方が-極)を表し、「キザキザと折れまがった記号」が、抵抗(2)を表しています。
そして、その二つの物(電池、抵抗)を直線で結んでいますが、これが、電線を表しています。
電流は、電池の+の方向から、抵抗を通って、電池の-の方向に戻ってきて、再び、電池の+から出るという形で、回路を巡る事になるわけです。
このように記号で組み合わせた図を回路図と呼びます。
回路図は、回路を記号を利用して、簡便化して表現したもの(3)ですし、大事な事は、この回路図を使って、元の回路を作る事ができる(4)事です。したがって、回路図を見ながら、回路を作り、実際に以下に述べるような色々な性質を実験で試して、確認する事(5)ができます。
「(数学以外の)科学」と「科学でないもの」を分けるのは、この「実験で試す事ができるかどうか?」です。実験で試す事ができないものは、普通は科学と呼べません。逆に、どんな「理屈」でも「実験で試す事ができる」ならば、「科学と呼んで構わないでしょう」。
ここで、敢て、「数学」を「科学」から分けているかというと、「数学」はある意味「現実を扱っているわけではない(「数学」以外の「科学」は、現実のものを扱っている)」からです。
つまり、「現実にはないかもしれない物も、数学では(むしろ積極的に?)扱います」。「現実にない」から「実験ができない」わけですが、
その代わりに、数学には「計算や証明」という「その事実を検証する」ために「実験に代る検証方法」が用意されているので、「科学と同類」と考えられているわけです。」
さて、オームの法則で説明したように、このような回路を作って電流を流すと、「抵抗に流れる電流の大きさ(I)は、抵抗の両端の電圧の大きさ(E)に比例し、抵抗の大きさ(R)に反比例する」と説明ました。つまり、式で表すと、「I = a×E ( aは比例定数で、正比例の関係)」,「I = b / R ( bは比例定数で反比例の関係)」という二つの事実を述べています。したがってまとめると、「I = c × (E/R) ( cは比例定数)」となります。そこで、単位を上手く定め(6)て、それぞれ、電圧(E)の単位はV (ボルト)、電流の量(I)の単位は、A (アンペア)、そして抵抗の大きさ(R)の単位はΩ(オーム)と定める事により、先の比例定数が1になり(7)オームの法則は、「I=E/R」という単純な形(8)になります。
例えば、1Ωの抵抗の両側の電圧(電位差)が1 Vであれば、その抵抗に流れる電流は1A (=1V/1Ω)となるという事ですし、もし、3Ωの抵抗の両側の電圧(電位差)が1.5 Vであれば、その抵抗に流れる電流は0.5A(1.5V/3Ω)となるという事です。
ここで、注意して欲しい事は、オームの法則は、「抵抗のある場所」でのみ成立する性質だという事です。では、抵抗以外の回路の他の部分はどうゆうふうになっているのでしょうか?
ここで「単位を上手く定める」という行為も、科学の世界ではよく行われています。というか、正確な言い方をすれば、幾つかの物(この場合は、E, I, Rの三つ)の間に関係(この場合は、オームの法則)があった場合、「その内の一つの単位を他の単位から、その法則を利用して『定義(そのように改めて定める)』する事」によって、「係数を単純(この場合は1)にする事ができる」ので「その方が計算が楽(つまり「上手い」)になる」から、そうする事が多いわけです。
どんなに偉い学者(だからこそ?)でも計算は楽な方が嬉しいわけです。
しかし、色々な理由から何時でもそのようにできるわけではありません。その理由が歴史的なものである(つまり、独立にそれぞれ、単位が定められて、後になって関係が見付かったので、やろうと思えばできるけどそうすると、これまでの記述を変更しなきゃいけないので面倒だからやらない場合。例えばジュール定数などは、エネルギーを定めるのに、仕事と熱が最初に区別されていたために、別々に同じエネルギーの単位に異なるものを利用していたために導入されることになった。)場合は段々と是正されてゆきますが、本質的に「それらの量が独立である(例えば、光の速度や、重力定数、電子の持つ電荷の量などがそうらしい? )」ものもあり、その場合は、係数が1にならず、面倒な数を覚える必要があります。
だから、覚えやすいし、計算しやすいですね。その代わりといってはなんですが、新しい単位(Ω)を覚えなければなりません。どうも「全てにおいて便利に」とはならないようです。
しかし、「単位」というのは、「どの大きさにするか?」より「皆が同じ大きさを利用する」事が本質的なので、もし、「結局、何かに决めなければならないのであれば、都合が良い形に决めちゃえ」という事なわけですね。
電気回路には、次のような幾つかの性質があります。
例えば、回路図の左側にある電線は、電池の+極と、抵抗の左を結んでいますが、この電線の中では、電位が変らないという規則なので、電池の+極の電位と抵抗の左の電位は同じになります。
同様に、右側にある電線は、電池の-極と、抵抗の右を結んでいますので、電池の-極の電位と抵抗の右の電位は同じになります。
電池の+極は、その-極に比べて、電位が高くなります。その電位差、すなわち電圧を作るという能力を電池はもっているわけです。電池はその能力(起電力)が一定になるように工夫されており、よく売られている電池は、1.5Vになっています。
元々の-極の電位が、幾つかは知る必要がないのですが、もし、それが5.0Vであれば、+の電位は、1.5Vの電池の場合、6.5V ( = 5.0V + 1.5V )になります。また、-極の電位が-1.0 Vであれば、+極の電位は+0.5 ( = -1.0V + 1.5V )になります。
これらの規則は、回路の中で、矛盾があってはなりません(13)。
例えば、電池の起電力を1.5V,抵抗を3Ωとするならば、回路図において、もし、電池の-極の電位が0.0Vであれば、電池の+極は、電池の規則により+1.5V (0.0V + 1.5V)にならなければなりません。そして、その電池の+極と、抵抗の左が電線で結ばれている、抵抗の左は、やはり同じ+1.5Vとなり、その抵抗に電流が、左から右に0.5Aの大きさで流れているのであれば、それによって、1.5V (= 3Ωx 0.5A)の電圧低下がおき、その抵抗の右はその分だけ電圧が低くなるので、0.0V ( = 1.5V - 1.5V )となるわけです。そして、その抵抗の右は、電池の-極と電線で結ばれているので、同じく0.0Vとなり、すべての場所で、上記の全ての規則が守られている事が判ります。
特に面白いのは、この規則から、「抵抗を流れる電流の量が0.5Aでなければならない」という事が「導けること」です(14)。つまり、もし、「抵抗を流れる電流の量が0.5Aでない(例えば2A)」とすると、抵抗のところで生じきる電圧降下は、オームの法則から6.0V (= 3Ωx 2 A)でなければならず、すると、抵抗の右の電位は、1.5V - 6.0V = -4.5Vとなってしまい、電池の-極の電位と一致しなくなってしまいます。
回路を構成することにより、電池の電圧が、抵抗の電圧と関係し、抵抗の電圧が定まったので、電流も定まったという仕組になっているわけです。
つまり、電池の+極も-極も、そして、抵抗の左の部分も右の部分も(それから、電線の中のどの部分も、抵抗の中も、電池の中も.. )すべて同じ電流の量が流れているということです。
これは、ちょっと気持が悪いかもしれません。なんとなく、これまでの説明から、坂のところ、つまり、抵抗のところでは電流が速く流れる(坂になっているので.. )し、そうでないところは緩やかに流れるような気がします。
実際に河の流れはそうですから。
しかし、ちょっと考えてみてください。ストローでジュースを飲む場合、口のところで一生懸命吸うからといって、ストローの口に近い部分は沢山ジュースが流れ、ジュースの近くではゆっくりと流れるという事はありません。
何が違うのでしょうか?実は、それは水の流れが、閉じ込められている(15)か、それとも閉じ込められていない(つまり開かれている)かどうかと関係があります。
河の流れは閉じ込められていないので、流れを促進する力(この場合は傾斜)が大きければ、速くなり、そうでなければ緩やかになります。
ところがストローの中の水は、そうは行ません。なぜなら、閉じ込められているので、どこかの部分だけ速く進もうとしても前は詰っていますし、後は空いてしまいます。閉じ込められている状態では、詰る事も空ける事もできませんから、結局、ストローのどこであっても、同じ速度で動かざるを得ないという事になりあす。
考えてみると、河の場合であっても、とうぜん、そのような事があるわけですが、開かれているので、水の流れの遅い所から急な所になる場合は、後が空くのではなく、急な場所の河幅が狭くなります。そして、逆の所では川幅が広くなる(三角州を思い浮べてください.. )だけで、「河の中を流れる水の量が変化しているわけではない(速度は変っても幅が狭くなるので結局は同じ量だけ流れている)」のです。
もちろん、閉じ込められている場合は、幅を広くしたり狭くできないので、結局、速度は同じ。それは、坂の場合も平らな場合も同じという事(16)です。
電流の場合も、電線の中に閉じ込められており、電線の外には出られないようになっていると考えれば、その閉じ込められた回路の中では、どこでも同じ量の電流がなければならないという事が判ります。
これも水の流れの例えから直観的には当然のような気がします(17)。前節と同様、電流は、電荷の流れであり、電流は電線の中だけに閉じ込められているので、分岐点では、その分岐点に入っている来る電荷の量と出て行く電荷の量は同じでなければ(18)なりません。
この性質の事を「キルヒホッフの第一法則(電流則)」と呼びます。
が、実は、例によって逆で、このように「どの場所でも同じ量の電流が流れているという」状態を、「直流電流が流れている」と呼んでおり、「抵抗値や、電圧を一定値にする事により『直流電流が流れている』ようにしてある」だけです。
まあ、確かに、直流回路で、抵抗値が変化せず、電圧も変化しないのであれば、オームの法則により、電流量も変化しないわけですが...
上記の回路の基本的な性質を利用すると、回路内での電圧や電流、そして抵抗の量を他の情報から求める事ができます。丁度、連立方程式のようなもの(19)で、回路の中にあるものの間の関係を利用して、計算を行います。
まずは、基本ということで、一つの電池と一つの抵抗からなる一番簡単な直流回路について。
まず、考えて欲しいのは、この回路には分岐点がありませんので、どこでも同じ電流(I)が流れているという事です。電位に関していえば、二つの電線(「電池の+側から抵抗の左まで」と、「抵抗の右から電池の-極まで」)に別れています。
この場合、この回路に拘る量は、回路をの何処でも流れる電流Iと、電池の起電力(電池の-極と+極の電位差つまり、電圧) E、そして、抵抗の大きさRです。
この場合も抵抗の所で、オームの法則が成立することを利用します。すると、もし、抵抗がRで電流がIであれば、抵抗の両端の電位差(電圧) Eは、「I=E/R」でなければなりません。
すると、これから「E=I×R」となることが判ります。
やはり、抵抗の部分を考えます。すると、もし、回路を流れる電流がIで電池の起電力がEであれば、抵抗Rとの関係は、「I=E/R」でなければなりません(何時もと同じ)。
すると、これから「R=E/I」となることが判ります。
今度は回路にある電池を二つにしてみよう。同じ物の回路でのつなぎ方には二種類方法がありますが、こでは、直列という接続方法(もう一方は、この後すぐに説明する)の方を示します。
電池の直列接続というのは、二つの電池(A,Bとしましょう..)一方(A)の-極に他方(B)の+極をつなぎます(図[電池の直列接続] :左の電池Aとよび、右の電池をBと呼ぶ事にする)。
.files/2batteries.gif)
そうすると、なんだか、+と-をつないだので、そこで、なにかが消えてしまうようにみえますが実際にはそうはなりません(20)。
先程の電圧の性質の電池の所で説明したように、電池の両側で-極から+極に電位を引き上げる能力(起電力)をもっているというだけです。
この図では、電球が抵抗に相当します。回路としては、三つのものをつないでいるので、三本の電線が必要になり、それらが電位をもっています。一本目は、Aの+の極と、抵抗(というか豆電球ですが..)の左を接続する電線(aと呼ぶ)。二本目は、抵抗の右とBの-極を接続する電線(bと呼ぶ)。そして最後の三本目は、問題のAの-極とBの+極を結んだ電線(cと呼ぶ)です。
一つ目の電池の起電力をE_1,二つ目の電池の起電力をE_2としましょう。
今、Bの-極の電位を例によって0とすると、Bの+極の電位はE_1の筈です(電池Bは起電力がE_2なので、その分電位があがる)すると、cの電位もE_1です。これが、Aの-極につながっているので、Aの-極の電位もE_2となります。Aの起電力は、E_1ですから、Aの+電位は、-の電位E_2に更にE_1を足してE_1 + E_2になるわけです。
すると、抵抗の両側の電位は、右が0で、左がE_1 + E_2ですから、その差の電圧はE_1 + E_2となります。
結局、電池は、同じ方向に直列に接続すると、電圧が加えられる(21)という事です。この事は、これによって、豆電球の灯が明るくなる、つまり、より多くのエネルギーが取り出される事にっている事からも判り、電流(抵抗は変っていませんから、電圧が大きくなった分)が大きくなっている事が判ります。
例えば、1.5Vの電池を二つ直列につなぐと1.5V + 1.5Vで3.0Vの電池と同じように振舞います。
+や-と呼んでいるのは、同じ電池の両側にあって初めて意味をもっているわけで、単独で+だったり-だったりするという話ではありません。
ちょうど右手と左手をつないだからといって、そのつないだ手を「真中手」とは呼ばないように..
むしろ逆に、同じ起電力をもった二つの電池の+極と+極、-極と-極を接続した直列回路を作ると、「あたかも電池がなかった」かのように振舞います。つまり、回路の中には、電流が全く流れなくなります。なぜ、そうなるかは、以下の説明を読んでかんがえてみましょう。
今度は、電池の+側同士、-側同士をつないでおきます(図[電池の並列接続])。すると、今度は、回路に合流地点が現れます。合流地点で、線は3本なりますが、電位は、導線の中ではどこも同じになります。
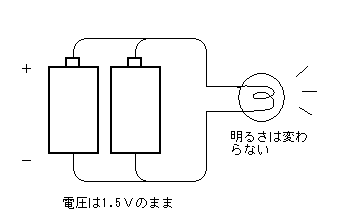
するとAの+極とBの+極は、同じ電位でなければなりません。更に-極も同じです。という事はAの起電力と、Bの起電力が同じでなければいけないという事になります。
ここでは、そうする(22)事にしましょう。
すると、抵抗の両端の電圧は、その等しい二つの電池の起電力と同じなので、電流も電池が一つの場合と同じ、すなわち、豆電球の明るさが変らないという事です。
折角、二つ電池をつないでいるのに、結果が変らないというのは、どうなっているのでしょか?完全に無駄なのでしょうか?
実は、そうではありません。確かに、抵抗を流れる電流の量は変っていません(抵抗も電圧も変っていないから..)。その結果として、電球で消費される電力(電圧×電流)も同じままです。
しかし、電池の方を考えてみましょう。電池が一つの場合は、この電力は、電池でも同じです。
ところが、今回の場合は、電線に分岐があるので、分岐の所から抵抗まではIだけ流れていたとしても、分岐から電池の所には、二つに別れていますので、電流の量も二つI_A ( Aの電池を流れる)とI_B ( Bの電池を流れる)に別れます。もちろんキルヒホッフの第一法則(電流則)からI = I_A + I_Bです(23)。AもBも起電力同じなので、電圧はEすなわち、「I×E = (I_A + I_B)×E = I_A×E + I_B×E」となります。つまり、電池Aが作る電力は、一つの場合はI×Eだったのだが、この場合はI_A×Eとなり少し減ります、同時に、電池BもI_B×Eとなり、どうように減ります。その結果として、「個々の電池の消耗がへり、全体として長もちするようになる」、つまり、「それだけ長く光るので結果的に多くの光を出す」という事になります。まさに、電池は、電気ではなく、電気エネルギーを溜めていることもこれから判ります。
しかし、「違っていたらどうするの..?」と考えますよね。その通りです。もちろん、起電力の違っている電池を並列に繋ぐ場合もありえますし、起電力の違う電池を並列につごうとしたら、電池が嫌がって逃げるなんて事も聞いたことがありません。
では、「実際についだら何が起きるか」ということですが、その場合には、「あたかも、電池の中に抵抗があらかじめ入っていたかのように振舞い」ます。これを「電池の内部抵抗」と呼びます(というか、正確に言えば、おしなべて、電気を流すものは全て抵抗を持つと思って良いでしょう[超伝導を除く]。その意味でも電線だって、僅かですが抵抗を持っています。ただ、それがとても小さいので、普段はあるのに気がつかない、あるいは余りに小さいので普段は無視してもも構わないという事です。ただ、もちろん「塵も積れば」という事があるのですが...)。
こう考えると、どうなるかと言えば、それぞれ異なる起電力を持つ、例えば-極が同じ電位で、Aの方が2V, Bの方が3Vとします。すると、Bの方により多くの電流が流れ、Bの中の抵抗のために、電位降下がおき、結局、Bの+極は3Vより小くなってしまいます。
一方、Aの方は、本来より電流の量が少いため、内部の抵抗による電圧降下がへり、それがあったから2Vになるはずだったのに、その降下が少いために2Vより電位差が大きくなります。その結果、+側の電位が高くなり、電位がそろうということです。
この議論をするには、電池の中の内部抵抗が何Ωかを考えねばないませんので、複雑になってしまい、ここでは割愛するという事です。
ただし、こうやって考えると、電池の「真の起電力」は、「回路につないだ時の電池の作る電圧より大きい(内部抵抗に打ち勝って電圧を作るため..)」のですが、以下では、内部抵抗の事は考えず、「電池の起電力」=「電池を回路につないだときの電圧」とするという事です。
これは、よく見掛ける構図(図[抵抗の直列接続])です。

この図でも、やはり電線が三本あります。ポイントは、二つの抵抗に間にある電線の電位でしょう。
その電位ですが、まずは、この回路が例によって一つの道しかないので、ここを通る電流の大きさIは種類しかないという事に注意しましょう。そこで、夫々の抵抗の大きさをR_1, R_2とすれば、それぞれの抵抗の両端で、生じる電圧降下は、それらに、共通の電流量であるIをかけて、それぞれ、I × R_1, I × R_2となります。つまり、抵抗の真中の電位は、左の電位よりI × R_1だけ低く、右の電位よりI × R_2だけ高いという事になります。
したがって、左の抵抗の左と右の抵抗の右の間の電圧は、結果的に(I × R_1 + I × R_2) = I × (R_1 + R_2)となります。一方、これは唯一の電池の起電力Eに等しいので、「E = I × (R_1 + R_2)」となります。これは考えてみると、「E/I = R_1 + R_2」という事です。すると、これを図[一番簡単な直流回路]と比較すると、丁度こちらの一つの抵抗が「R=E/I」となるわけですから、この部分と、この二つの抵抗を直列に並べた部分(R_1+R_2)が同じ役割を果している事がわかります。
つまり、二つの抵抗R_1とR_2は、直列につなぐとR_1+R_2の大きさをもった抵抗と同じ振舞いをするという事です。
これも、よく見掛ける構図(図[抵抗の並列接続])です。

こちらの場合は、今度は、電線が分岐しているので、電流がそこで分れます。問題は、「どのような割合で電流が分れるか」という事です。
一方、電位で考えると二つの部分しかありません。つまり、電池の起電力Eは、すなわち、R_1, R_2の起す二つの電圧降下の双方に等しいという事になります。
この事から、R_1, R_2を通る電流をI_1, I_2とすれば、それぞれ、「E=I_1 × R_1, E=I_2 × R_2」となります。つまり、「I_1 = E/R_1, I_2 = E/R_2」となります。これは、かなり納得の行く結果で、抵抗が小さい方には、多くの電流が流れる(24)という事です。もちろん、電池を通る電流Iは、この二つの電流が合流しているので「I=I_1+I_2」が成立します。
一方、この二つの抵抗全体も、もちろん、一つの抵抗Rのように振舞うわけですが、そのRも求めてみましょう。この全体のRの電圧降下は、電池を通る電流Iを使って「R × I」で表現できます。これが電圧の起電力Eと同じなので「E = R × I」です。つまり、「E = R × I = R × ( I_1 + I_2 ) = R × ( E/R_1 + E/R_2 )」となります。そこで両辺を「E/R_1 + E/R_2」でわると、Eが約分できて「R = 1/( 1/R_1 + 1/R_2 ) = (R_1 × R_2)/(R_1 + R_2)」というちょっと複雑な式(並列に接続した二つの抵抗の抵抗値を求める公式)がでてきます。これは、もっとシンプルに両辺の逆数を取って「1/R = 1/R_1 + 1/R_2」とする場合もあります。
具体的な例で試してみましょう。E = 6V, R_1 = 2Ω, R_2 = 3Ωとします。まず、「I_1 = E/R_1 = 6V/2Ω= 3A, I_2 = E/R_2 = 6V/3Ω= 2A」となります。すると、全体を流れる電流IはI = I_1 + I_2 = 5Aとなります。したがって、抵抗Rは、R = E/I = 6V / 5A = 1.2Ωとなるわけです。
これを最後に求めた公式で計算すると、R = ( 2 × 3 ) / ( 2 + 3 ) = 6/5 = 1.2Ωとなり、確かに結果が一致するという事が確かめられます。
次のような複雑な回路(図[複雑な抵抗の接続例])を考えてみましょう。たしかに計算は大変ですが、原理はこれまでと全く同じです。
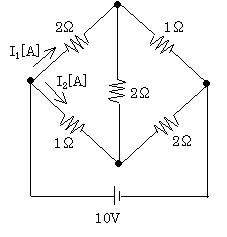
まず、電位を考えてみます。電池の右側を0.0Vとすれば、10.0Vになります。また、抵抗に挟まれた上の合流点の電位と、下の合流点の電位は、すぐには解らないので、E_1, E_2としておきましょう。
そして、電池を通る全体の電流の大きさはI、また、左の上の2Ωの抵抗を通る電流と、左下の1Ωの抵抗を左から右に流れる電流の量には、それぞれ、図にI_1, I_2と図示されていますが、これに合せて、右上の1ΩにはI_3,左下の2ΩにはI_4,そして最後に、真中の2Ωの抵抗を流れる電流を、恐らく下から上に流れるとして(25)、その電流の量をI_5とすることにします。
さて、
次に、分岐点における電流の関係に着目すると次のような式がでます。
ただし、最後の式は、結局、上記の三つから導けるので、意味がなく、取り除いて考えます。
すると、これらは連立方程式なので、解く事ができ、これを解くと、次のような結果になります。
そして、全体の抵抗値RはR = E/I = 10.0V/7.0A = 10/7Ωとなります。